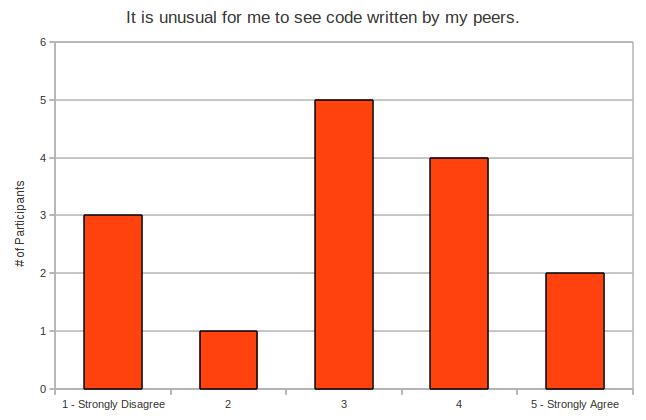
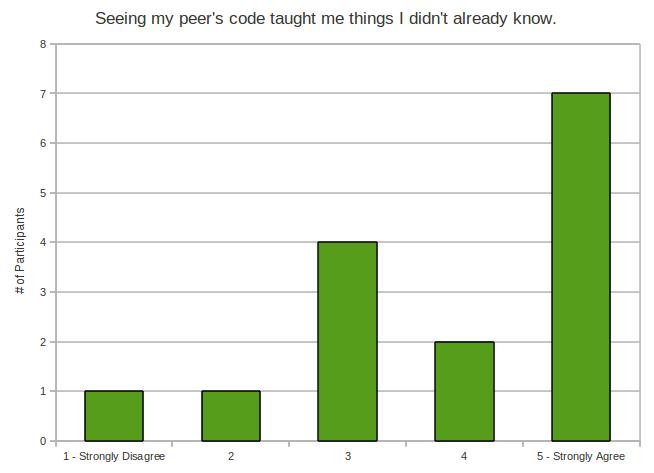
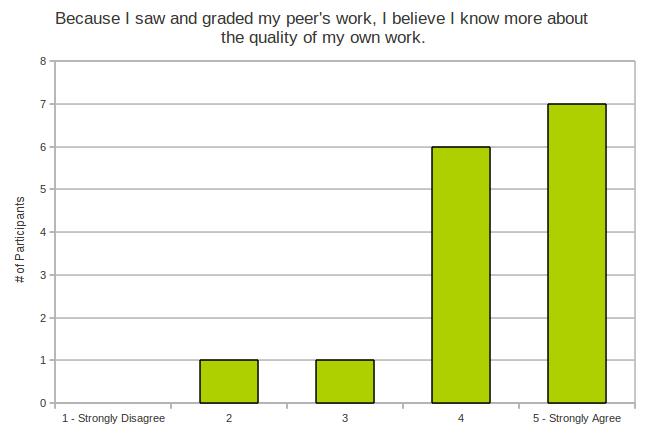
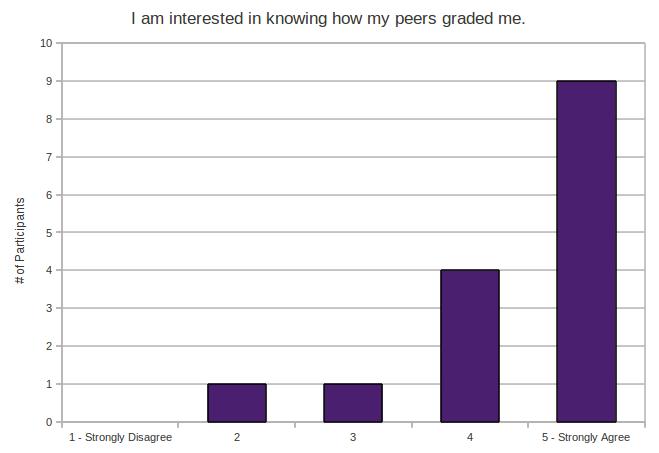
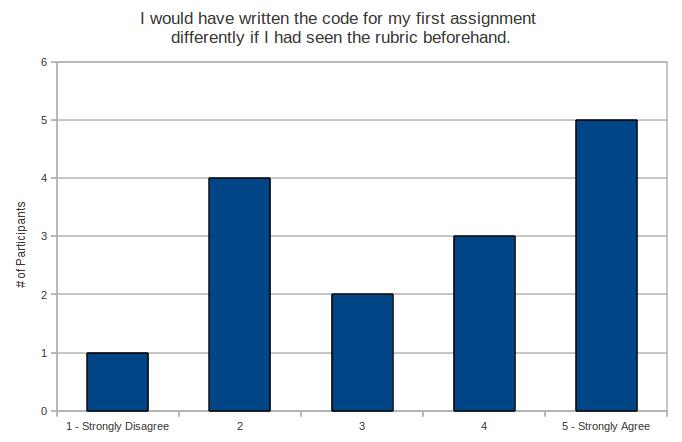
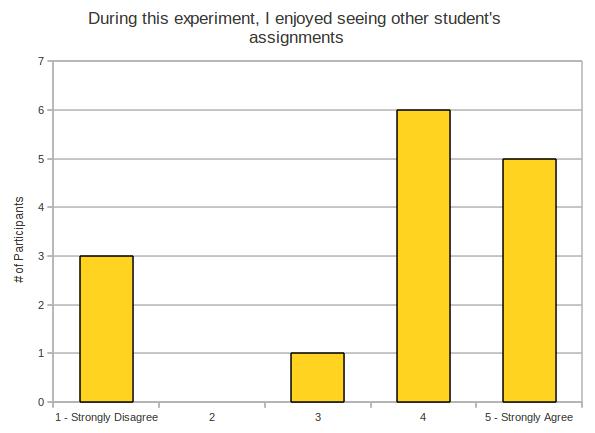
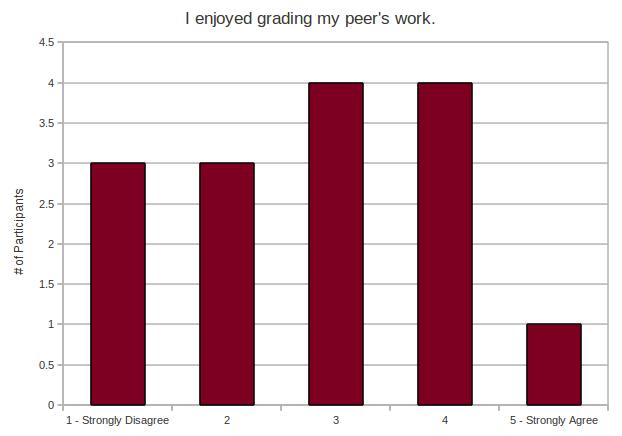
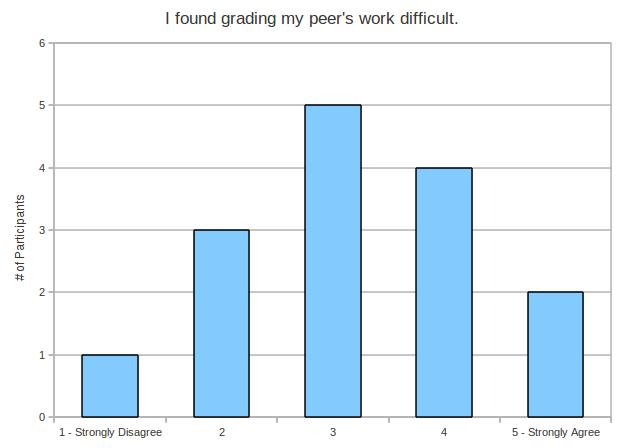
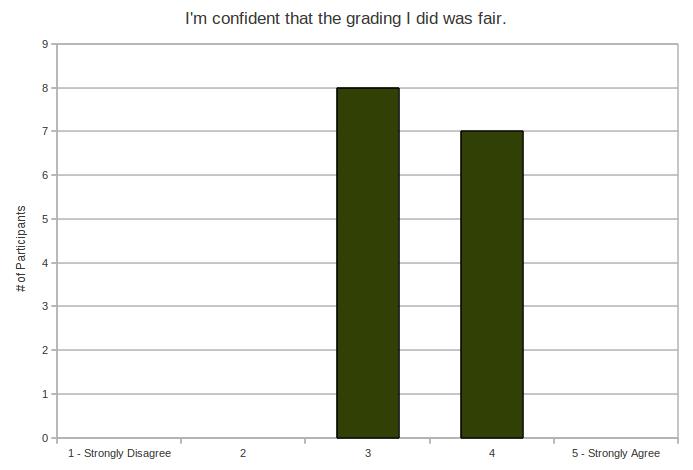
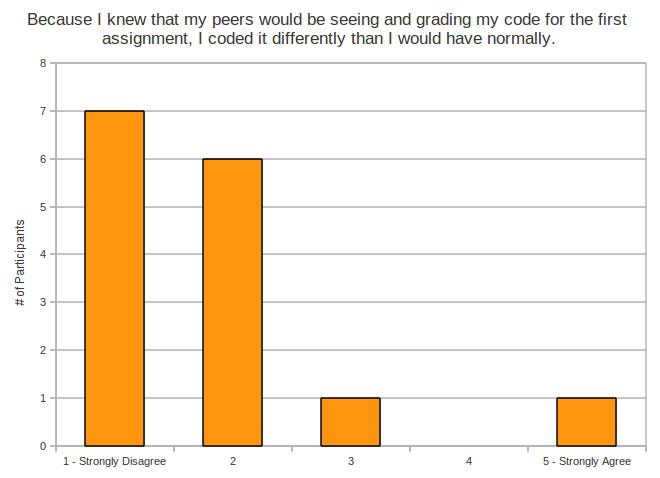
My experiment makes a little bit of an assumption – and it’s the same assumption most teachers probably make before they hand back work. We assume that the work has been graded correctly and objectively.
The rubric that I provided to my graders was supposed to help sort out all of this objectivity business. It was supposed to boil down all of the subjectivity into a nice, discrete, quantitative value.
But I’m a careful guy, and I like back-ups. That’s why I had 2 graders do my grading. Both graders worked in isolation on the same submissions, with the same rubric.
So, did it work? How did the grades match up? Did my graders tend to agree?
Sounds like it’s time for some data analysis!
About these tables…
I’m about to show you two tables of data – one table for each assignment. The rows of the tables map to a single criterion on that assignments rubric.
The columns are concerned with the graders marks for each criterion. The first columns, Grader 1 – Average and Grader 2 – Average, simply show the average mark given for each criteria for each grader.
Number of Agreements shows the number of times the marks between both graders matched for that criterion. Similarly, Number of Disagreements shows how many times they didn’t match. Agreement Percentage just converts those two values into a single percentage for agreement.
Average Disagreement Magnitude takes every instance where there was a disagreement, and averages the magnitude of the disagreement (a reminder: the magnitude here is the absolute value of the difference).
Finally, I should point out that these tables can be sorted by clicking on the headers. This will probably make your interpretation of the data a bit easier.
So, if we’re clear on that, then let’s take a look at those tables…
Flights and Passengers Grader Comparison
[table id=6 /]
Decks and Cards Grader Comparison
[table id=7 /]
Findings and Analysis
It is very rare for the graders to fully agree
It only happened once, on the “add_passenger” correctness criterion of the Flights and Passengers assignments. If you sort the tables by “Number of Agreements” (or Number of Disagreements), you’ll see what I mean.
Grader 2 tended to give higher marks than Grader 1
In fact, there are only a handful of cases (4, by my count), where this isn’t true:
- The add_passenger correctness criterion on Flights and Passengers
- The internal comments criterion on Flights and Passengers
- The error checking criterion on Decks and Cards
- The internal comments criterion on Decks and Cards
The graders tended to disagree more often on design and style
Sort the tables by Number of Disagreements descending, and take a look down the left-hand side.
There are 14 criteria in total for each assignment. If you’ve sorted the tables like I’ve asked, the top 7 criteria of each assignment are:
Flights and Passengers
- Style
- Design of __str__ method
- Design of heaviest_passenger method
- Design of lightest_passenger method
- Docstrings
- Correctness of __str__ method
- Design of Flight constructor
Decks and Cards
- Correctness of deal method
- Style
- Design of cut method
- Design of __str__ method
- Docstrings
- Design of deal method
- __str__
Of those 14, 9 have to do with design or style. It’s also worth noting that Doctrings and the correctness of the __str__ methods are in there too.
There were slightly more disagreement in Decks and Cards than in Flights and Passengers
Total number of disagreements for Flights and Passengers: 136 (avg: 9.71 per criterion)
Total number of disagreements for Decks and Cards: 161 (avg: 11.5 per criterion)
Discussion
Being Hands-off
From the very beginning, when I contacted / hired my Graders, I was very hands-off. Each Grader was given the assignment specifications and rubrics ahead of time to look over, and then a single meeting to ask questions. After that, I just handed them manila envelopes filled with submissions for them to mark.
Having spoken with some of the undergraduate instructors here in the department, I know that this isn’t usually how grading is done.
Usually, the instructor will have a big grading meeting with their TAs. They’ll all work through a few submissions, and the TAs will be free to ask for a marking opinion from the instructor.
By being hands-off, I didn’t give my Graders the same level of guidance that they may have been used to. I did, however, tell them that they were free to e-mail me or come up to me if they had any questions during their marking.
The hands-off thing was a conscious choice by Greg and myself. We didn’t want me to bias the marking results, since I would know which submissions would be from the treatment group, and which ones would be from control.
Anyhow, the results from above have driven me to conclude that if you just hand your graders the assignments and the rubrics, and say “go”, you run the risk of seeing dramatic differences in grading from each Grader. From a student’s perspective, this means that it’s possible to be marked by “the good Grader”, or “the bad Grader”.
I’m not sure if a marking-meeting like I described would mitigate this difference in grading. I hypothesize that it would, but that’s an experiment for another day.
Questionable Calls
If you sort the Decks and Cards table by Number of Disagreements, you’ll find that the criterion that my Graders disagreed most on was the correctness of the “deal” method. Out of 30 submissions, both Graders disagreed on that particular criterion 21 times (70%).
It’s a little strange to see that criterion all the way at the top there. As I mentioned earlier, most of the disagreements tended to be concerning design and style.
So what happened?
Well, let’s take a look at some examples.
Example #1
The following is the deal method from participant #013:
def deal(self, num_to_deal):
i = 0
while i < num_to_deal:
print self.deck.pop(0)
i += 1
Grader 1 gave this method a 1 for correctness, where Grader 2 gave this method a 4.
That’s a big disagreement. And remember, a 1 on this criterion means:
Barely meets assignment specifications. Severe problems throughout.
I think I might have to go with Grader 2 on this one. Personally, I wouldn’t use a while-loop here – but that falls under the design criterion, and shouldn’t impact the correctness of the method. I’ve tried the code out. It works to spec. It deals from the top of the deck, just like it’s supposed to. Sure, there are some edge cases missed here (what is the Deck is empty? What if we’re asked to deal more than the number of cards left? What if we’re asked to deal a negative number of cards? etc)… but the method seems to deliver the basics.
Not sure what Grader 1 saw here. Hmph.
Example #2
The following is the deal method from participant #023:
def deal(self, num_to_deal): res = [] for i in range(0, num_to_deal): res.append(self.cards.pop(0))
Grader 1 gave this method a 0 for correctness. Grader 2 gave it a 3.
I see two major problems with this method. The first one is that it doesn’t print out the cards that are being dealt off: instead, it stores them in a list. Secondly, that list is just tossed out once the method exits, and nothing is returned.
A “0” for correctness simply means Unimplemented, which isn’t exactly true: this method has been implemented, and has the right interface.
But it doesn’t conform to the specification whatsoever. I would give this a 1.
So, in this case, I’d side more (but not agree) with Grader 1.
Example #3
This is the deal method from participant #025:
def deal(self, num_to_deal):
num_cards_in_deck = len(self.cards)
try:
num_to_deal = int(num_to_deal)
if num_to_deal > num_cards_in_deck:
print "Cannot deal more than " + num_cards_in_deck + " cards\n"
i = 0
while i < num_to_deal:
print str(self.cards[i])
i += 1
self.cards = self.cards[num_to_deal:]
except:
print "Error using deal\n"
Grader 1 also gave this method a 1 for correctness, where Grader 2 gave a 4.
The method is pretty awkward from a design perspective, but it seems to behave as it should – it deals the provided number of cards off of the top of the deck and prints them out.
It also catches some edge-cases: num_to_deal is converted to an int, and we check to ensure that num_to_deal is less than or equal to the number of cards left in the deck.
Again, I’ll have to side more with Grader 2 here.
Example #4
This is the deal method from participant #030:
def deal(self, num_to_deal):
''''''
i = 0
while i <= num_to_deal:
print self.cards[0]
del self.cards[0]
Grader 1 gave this a 1. Grader 2 gave this a 4.
Well, right off the bat, there’s a major problem: this while-loop never exists. The while-loop is waiting for the value i to become greater than num_to_deal…but it never can, because i is defined as 0, and never incremented.
So this method doesn’t even come close to satisfying the spec. The description for a “1” on this criterion is:
Barely meets assignment specifications. Severe problems throughout.
I’d have to side with Grader 1 on this one. The only thing this method delivers in accordance with the spec is the right interface. That’s about it.
Dealing from the Bottom of the Deck
I received an e-mail from Grader 2 about the deal method. I’ve paraphrased it here:
If the students create the list of cards in a typical way, for suit in CARD_SUITS; for rank in CARD_RANKS, and then print using something like:
for card in self.cards
print str(card) + “\n”
Then for deal, if they pick the cards to deal using pop() somehow, like:
for i in range(num_to_deal):
print str(self.cards.pop())Aren’t they dealing from the bottom
My answer was “yes, they are, and that’s a correctness problem”. In my assignment specification, I was intentionally vague about the internal collection of the cards – I let the participant figure that all out. All that mattered was that the model made sense, and followed the rules.
So if I print my deck, and it prints:
Q of Hearts A of Spades 7 of Clubs
Then deal(1) should print:
Q of Hearts
regardless of the internal organization.
Anyhow, only Grader 2 asked for clarification on this, and I thought this might be the reason for all of the disagreement on the deal method.
Looking at all of the disagreements on the deal methods, it looks like 7 out of the 20 can be accounted for because students were unintentionally dealing from the bottom of the deck, and only Grader 2 caught it.
Subtracting the “dealing from the bottom” disagreements from the total leaves us with 13, which puts it more in line with some of the other correctness criteria.
So I’d have to say that, yes, the “dealing from the bottom” problem is what made the Graders disagree so much on this criterion: only 1 Grader realized that it was a problem while they were marking. Again, I think this was symptomatic of my hands-off approach to this part of the experiment.
In Summary
My graders disagreed. A lot. And a good chunk of those disagreements were about style and design. Some of these disagreements might be attributable to my hands-off approach to the grading portion of the experiment. Some of them seem to be questionable calls from the Graders themselves.
Part of my experiment was interested in determining how closely peer grades from students can approximate grades from TAs. Since my TAs have trouble agreeing amongst themselves, I’m not sure how that part of the analysis is going to play out.
I hope the rest of my experiment is unaffected by their disagreement.
Stay tuned.
See anything?
Do my numbers make no sense? Have I contradicted myself? Have I missed something critical? Are there unanswered questions here that I might be able to answer? I’d love to know. Please comment!