But first, a confession…

Sometimes I play a little fast and loose with my English.  If there’s anything that my Natural Language Processing course taught me last year, it’s that I really don’t have a firm grasp on the formal rules of grammar.

The reason I mention this is because of the word “peer”.  The plural of peer is peers.  And the plural possessive of peer is peers’.  With the apostrophe.

I didn’t know that a half hour ago.  Emily told me, and she’s a titan when it comes to the English language.

The graphs below were created a few days ago, before I knew this rule.  So they use peer’s instead of peers’.  I dun goofed.  And I’m too lazy to change them (and I don’t want to use OpenOffice Draw more than I have to).

I just wanted to let you Internet people know that I’ve realized this, since their are so many lot of grammer nazi’s out they’re on the webz.

Now, with that out of the way, where were we?

The Post-Experiment Questionnaire

If you read my experiment recap, then you know that my treatment group wrote a questionnaire after they were done all of their assignment writing.

The questionnaire was used to get an impression of how participants felt about their peer reviewing experience.

A note on the peer reviewing experience

Just to remind you, my participants were marking mock-ups that I created for an assignment that they had just written.  There were 5 mock-ups per assignment, so 10 mock-ups in total.  Some of my mock-ups were very concise.  Others were intentionally horrible and hard to read.  Some were extremely vigilant in their documentation.  Others were laconic.  I tried to capture a nice spectrum of first year work. None of my participants knew that I had mocked the assignments up.

Anyhow, back to the questionnaire…

The questionnaire made the following statements, and asked students to agree on a scale from 1 to 5, where 1 was Strongly Disagree and 5 was Strongly Agree:

1. It is unusual for me to see code written by my peers.
2. Seeing my peer’s code taught me things I didn’t already know.
3. Because I saw and graded my peer’s work, I believe I know more about the quality of my own work.
4. I am interested in knowing how my peers graded me.
5. I would have written the code for my first assignment differently if I had seen the rubric beforehand.
6. During this experiment, I enjoyed seeing other student’s assignments.
7. I enjoyed grading my peer’s work.
8. I found grading my peer’s work difficult.
9. I’m confident that the grading I did was fair.
10. Because I knew that my peers would be seeing and grading my code for the first assignment, I coded it differently than I would have normally.

For questions 2, 5, 7, 8, and 10, participants were asked to expand with a written comment if they answered 3 or above.

Of the 30 participants in my study, 15 were in my treatment group, and therefore only 15 people filled out this questionnaire.

The graphs are histograms – that means that the higher the bar is, the more participants answered the question that way.

So, without further ado, here are the results…

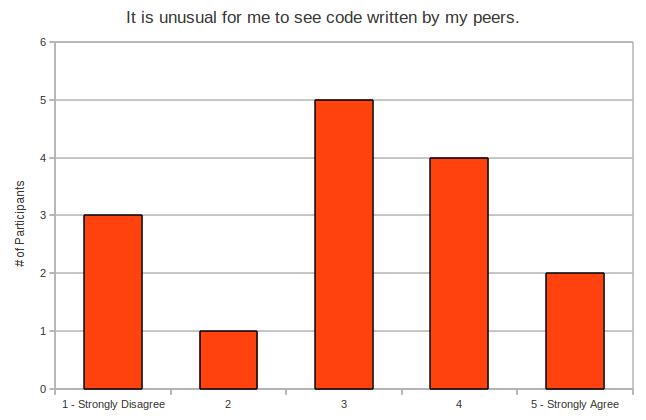
While there’s more weight on the positive side, opinion seems pretty split on this one.  It might really depend on what kind of social / working group you have in your programming classes.

It might also depend on how adherent students are to the rules, since sharing code with your peers is a bit of a no-no according to the UofT Computer Science rules of conduct.  Most programming courses have something like the following on their syllabus:

Never look at another student’s assignment solution, whether it is on paper or on the computer
screen. Never show another student your assignment solution. This applies to all drafts of a solution
and to incomplete solutions.

Of course, this only applies before an assignment is due.  Once the due date has passed, it’s OK to look at one another’s code…but how many students do that?

Anyhow, looking at the graph, I don’t think we got too much out of that one.  Let’s move on.

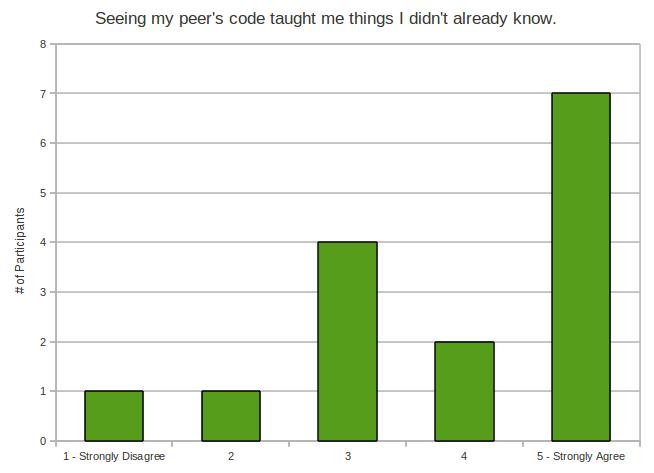
Well, that’s a nice strong signal.  Clearly, there’s more weight on the positive side.  So my participants seem to understand that grading the code is teaching them something.  That’s good.

And now for an interesting question:  is there any relationship between the amount of programming experience of the participant, and how they answered this question?  Good question.  Before the experiment began, all participants filled out a brief questionnaire.  The questionnaire asked them to provide, in months, how much time they’ve spent in either a programming intensive course, or a programming job.  So that’s my fuzzy measure for programming experience.

The result was surprising.

For participants who answered 5 (strongly agreed that they learned things they didn’t already know):

Number of participants:  7
Maximum number of months:  36
Minimum number of months:  4
Average number of months:  16

For participants who answered 4:

Number of participants:  1
Number of months:  16

For participants who answered 3:

Number of participants:  4
Maximum number of months:  16
Minimum number of months:  8
Average number of months:  13

For participants who answered 2:

Number of participants:  1
Average number of months:  5

For participants who answered 1 (strongly disagreed that they learned things they didn’t already know):

Number of participants:  1
Average number of months: 16

So there’s no evidence here that participants with more experience felt they learned less from the peer grading.

This was one of those questions where participants were asked to expand if they answered 3 or above.  Here are some juicy morsels:

If you answered 3 or greater to the question above, what did you learn?

I learned some tricks and shortcuts of coding that make the solution more elegant and sometimes shorter.

…it showed me how hard some code are to read since I do not know what is in the programmer’s head.

I learned how different their coding style are compared to mine, as well as their reasoning to the assignment.

l learned about how other people think differently on same question and their programming styles can be different very much.

one of the codes I marked is very elegant and clear. It uses very different path from others. I really enjoyed that code. I think good codes from peers help us learn more.

I didn’t know about the random.shuffle method.  I also didn’t know that it would have been better to use Exceptions which I don’t really know.

The different design or thinking towards the same question’s solution, and other ways to interpret a matter.

Other people can have very convoluted solutions…

Different ways of solving a problem

A few Python shortcuts, especially involving string manipulation. As well, I learned how to efficiently shuffle a list.

algorithm (ways of thinking), different ways of doing the same thing

Sometimes a few little tricks or styles that I had forgotten about.  Also just a few different ways to go about solving the problem.

So what conclusions can I draw from this?

It looks like, regardless of experience, students seem to think peer grading teaches them something – even if it’s just a different design, or an approach to a problem.

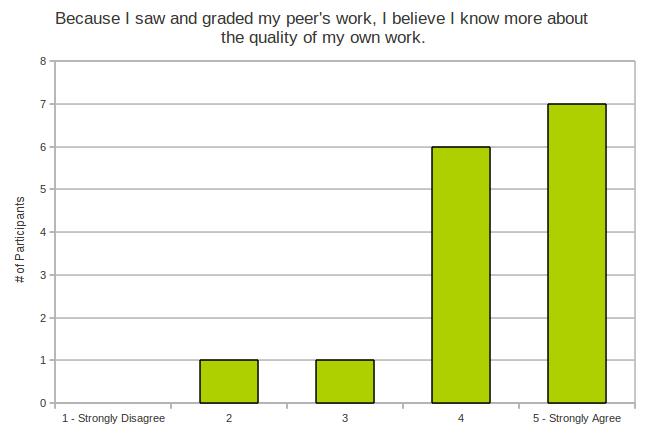
Another clear signal in the “strongly agree” camp.  This one is kind of a no-brainer though – seeing work by others certainly gives us a sense of how our own work rates in comparison.  We do this kind of comparison all the time.

Anyhow, my participants seem to agree with that.

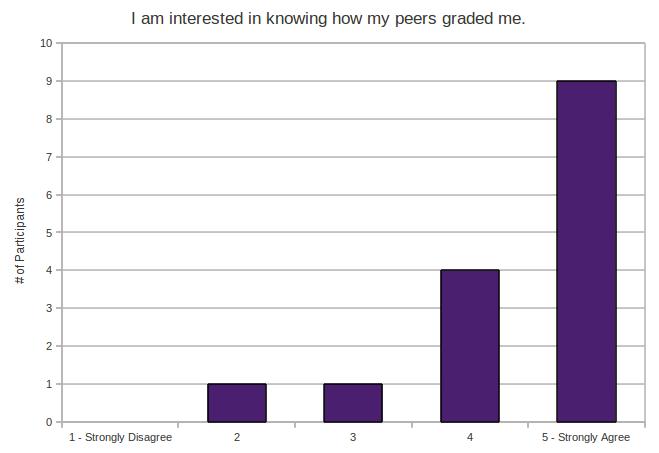
Again, a lot of agreement there.  Students are curious to know what their peers think of their work.  They care what their peers think.  This is good.  This is important.

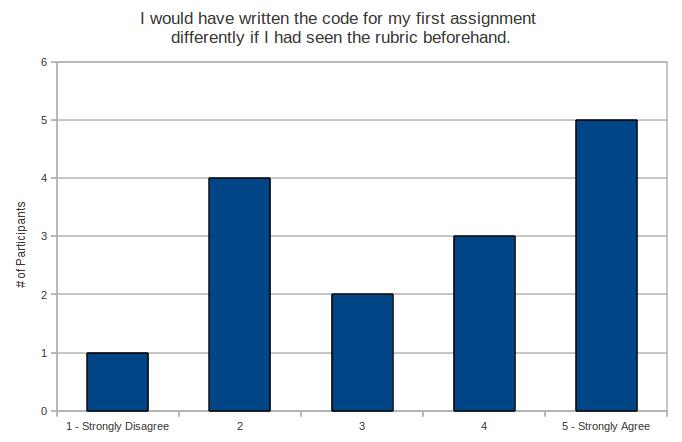
Hm.  More of a mixed reaction here.  There’s more weight on the “strongly agree” side, but not a whole lot more.

This is interesting though.  If I find that my treatment group does perform better on their second assignment, is it possible that their improvement isn’t from the grading, but rather from their intense study of the rubric?

So, depending on whether or not there’s an improvement, my critics could say I might have a wee case of confounding factor syndrome, here.

And I would agree with them.  However, I would also point out that if there was an improvement in the treatment group, it wouldn’t matter what the actual source of the learning was – the peer grading (along with the rubric) caused an improvement.  And that’s fine.  That’s an OK result.

Of course, this is all theoretical until I find out if there was an improvement in the treatment group grades.  Stay tuned for that.

Anyhow, this was another one of those questions where I asked for elaboration for answers 3 and up.  Here’s what the participants had to say:

If you answered 3 or greater to the question above, what would you have done differently?

I would have checked for exceptions (and know what exceptions to check). I would have put more comments and docstrings into my code. I would have named my variables more reasonably.

I would’ve wrote out documentation. (ie. docstrings) Though I found that internal commenting wasn’t necessary.

i’ll add more comments to my code and maybe some more exceptions.

Added comments and docstrings.

Code’s design, style, clearness, readability and docstrings.

Made more effort to write useful docstrings and comments

I would’ve included things that I wouldn’t have included if I was coding for myself (such as comments and docstrings).

Added more documentation (I forget what it’s called but it’s when you surround the comments with “” ”’ “”)

Written more docstrings and comments (even though I think the code was simple enough and the method names self-explanatory enough that the code didn’t need more than one or two terse docstrings).

I forgot about docstrings and commenting my code

So it sounds like evaluation on documentation wasn’t clear enough in my assignment specification.  There’s also some indication that participants thought that documentation wasn’t necessary if the code is simple enough.  With respect to Docstrings, I’d have to disagree, since Docstrings are overwhelmingly useful for generating and compiling documentation.  That’s just my own personal feelings on the matter, though.

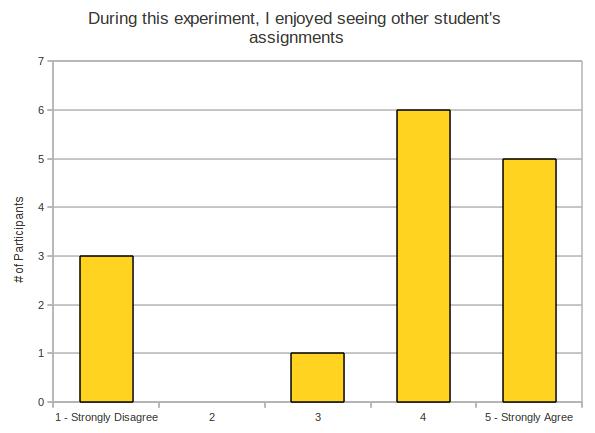
Note: this is not to be confused with “I enjoyed grading my peers’ work”, which is the next question.

Mostly agreement here.  So that’s interesting – participants enjoyed the simple act of seeing and reading code written by their peers.

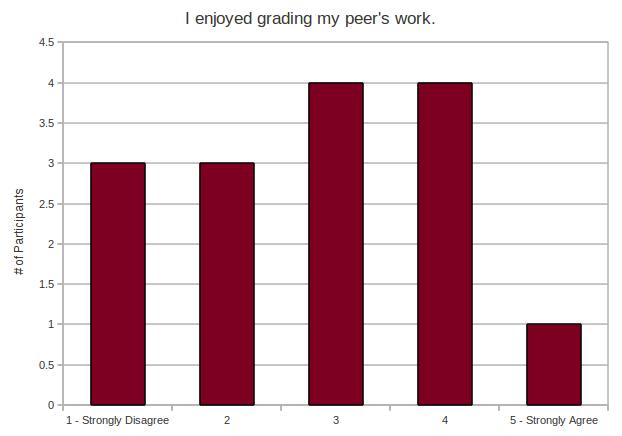
It looks like, in general, students don’t really enjoy grading their peers’ code. Clearly, it’s not a universal opinion – you can see there’s some disagreement in the graph.  Still, the trend seems to go towards the “strongly disagree” camp.

That’s a very useful finding.  There’s nothing worse than sweating your butt off to design and construct a new task for students, only to find out that they hate doing it.  We may have caught this early.

And I don’t actually find this that surprising:  code review isn’t exactly a pleasurable experience.  The benefits are certainly nice, but code review is a bit like flossing… it just seems to slow the morning routine down, regardless of the benefits.

Here’s what some participants had to say about their answers:

If you answered 3 or greater to the question above, why did you enjoy grading your peer’s work?

Because I like to compare my thoughts and other people’s thoughts.

well, some of the codes are really hard to read. But I did learn something from the grading. And letting students grade the codes is more fair.

I got to see where I went wrong and saw more creative/efficient solutions which will give me ideas for future assignments. But otherwise it was really boring.

So that I can learn from my peer’s thinking which gives me more diversity of coding and problem-solving.

Sometimes you see other student’s styles of coding/commenting/documenting and it helps you write better code. Sometimes you learn things that you didn’t know before. Sometimes it’s funny to see how other people code.

It was interesting to see their ideas, although sometimes painful to see their style.

not so much the grading part, but analyzing/looking at the different ways of coding the same thing

It gave me a rare prospective to see how other people with a similar educational background write their code.

Makes you think more critically about the overall presentation of your code.  You ask yourself : “What would someone think of my code if they were doing this?  Would I get a good mark?”

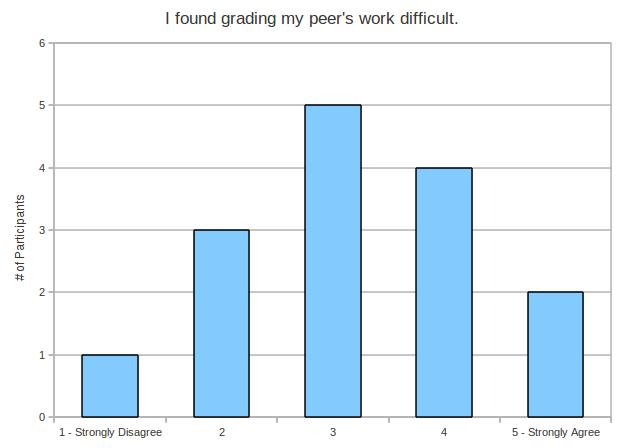
This one is more or less split right down the middle, with a little more weight on the agree side.

Again, participants who answered 3 or above were asked to elaborate.  Here are some comments:

If you answered 3 or greater to the question above, what about grading your peer’s work was difficult?

The hardest part was trying to trace through messy code in order to figure out if it actually works.

Emotionally, I know what the student is doing but I have to give bad marks for comments or style which makes me feel bad. Sometimes it is hard to distinguish the mark whether it is 3 or 4. The time was critical (did not have time to finish all papers) which might result in giving the wrong mark. I kept comparing marks and papers so I could get almost the fairest result between all students. It is hard to mark visually, i.e. not testing the code. Some codes are hard to read which make it hard for marking and I can assume it is wrong but it actually works.

Giving bad marks are hard!  Reading bad code is painful!  It wasn’t fun! 🙁

It just became really tedious trying to understand people’s code.

To test and verify their code is hard sometimes as their method of solving a problem might be complicated. I need to think very carefully and test their code progressively.

The rubric felt a little too strict. Sometimes a peer’s code had small difficulties that could easily be overcome, but would be labeled as very poor. Also, the rubric wasn’t clear enough, especially on the error handling portions and style. There could be many ways of coding for example the __str__ functions (using concatenation versus using format eg. ‘ %s’ % string as opposed to using + str(string) +)

I just found it hard to read other’s code because I already have a set idea of how to solve the problems. I did not see how the solutions of my peers would’ve improved my own solutions, so I did not find value in this.

Reading through each line of code and trying to figure out what it does

Reading through convoluted, circuitous code to determine correctness.

Not every case is clear-cut, and sometimes it’s hard to decide which score to give.

Being harsh and honest.  I guess it’s good not to ever meet the people who wrote the codes (unlike TAs) because they aren’t there to defend themselves.  Saves some headaches 🙂

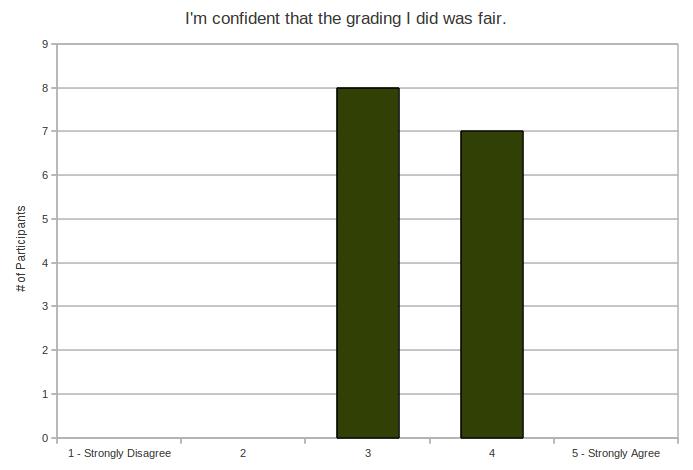
Ok, more or less full agreement here.  At least, no disagreement.  But also no full agreement.  It’s sort of a lethargic “meh” with a flaccid thumbs up.

The conclusion?  My participants felt that, more or less, their grading was probably fair.  I guess.

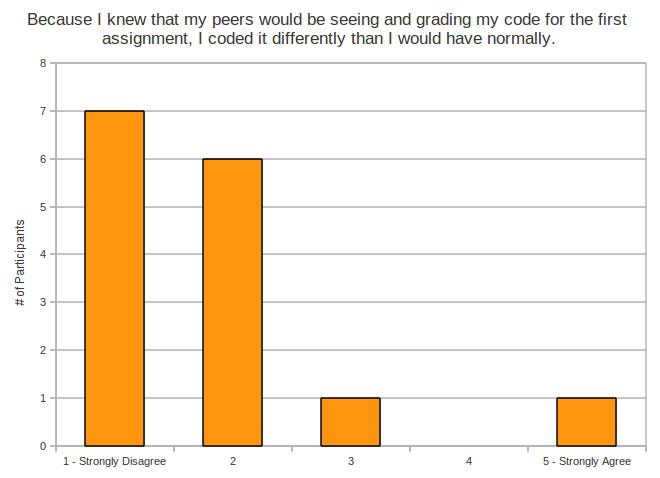
Now this one…

This one is tricky, because I might have to toss it out.  Each one of my participants was told flat out that other participants in the study may or may not see their code.  This is true, since the graders are also participants in the study.

However, I did not outright tell them that other participants would be grading their code for the first assignment.  So I think this question may have come as a surprise to them.

That was an oversight on my part.  I screwed up.  I’m human.

The two lone participants who answered 3 or above wrote:

If you answered 3 or greater to the question above, what did you do differently?

Making the docstring comments more clear, simplifying my design as possible, writing in a better style.

Added a bit more comments to explain my code in case peers don’t understand.

Anyhow, so those are my initial findings.  If you have any questions about my data, or ideas on how I could analyze it, please let me know.  I’m all ears.